Sorting Algorithm Visualizations
Considering that this project utilized Java, C++, Python, and JavaScript, I really ought to have put it in all of the categories on my site.
In the course of my study, I was treated to a brief overview of a few sorting algorithms. The unit covered insertion sort, selection sort, quick sort, and merge sort. I have a rather unfortunate history of having trouble with sorting algorithms; the ones that I wanted to implement the most were always the ones that were just beyond my grasp.
The best way to fully understand a sorting algorithm is, of course, to implement it yourself. As I also needed practice in Java, I thought it might be prudent to attempt to do so. The project quickly morphed into visualizing sorting algorithms, which finds itself right at home on my portfolio.
The sorting algorithms are implemented as static public members of a sorting class, where each algorithm receives as input only a LoggedArray. LoggedArray is a composition of ArrayList
A Python script takes the textual description and recreates the operations. It then uses the PIL and wave libraries to produce images and audio which can all be combined into the final video, which I use FFmpeg for. Below is the final video of all 14 algorithms.
The audio can get a bit high-pitched, headphone users beware!
Tournament Sort
Of all the algorithms, only two really stood out to me. The first was tournament sort (worse heap sort) and the second was smooth sort (better heap sort). Beginning with the duller of the two, tournament sort requires twice as much memory as the initial array occupies, although I'm sure that could be cut in half. As I was not strapped for RAM, I opted to actually round the list's size up to the nearest power of two and double that. This significantly reduces the amount of bookkeeping necessary.
The auxiliary array is essentially storing many successive rounds of what we might call a single-elimination tournament. The right half stores the top 50% of the original array. The right half of the remainder stores the top 25%, then the top 12.5%, and so on. The construction of this array is, of course, closely analogous to heapify(). The "champion" is then extracted from the left and we perform siftDown() findNewChampion() by observing the contenders for the top spot. We recursively call findNewChampion() on the old champion's place in this round of the tournament, replacing all log(n) instances of the champion in the auxiliary array with the next best element. The last instance is set to negative infinity (or 0 in my case, as my implementation sorts natural numbers).
The contender who previously lost is copied to the left-most spot and in the next round it is replaced, just like heap sort.
Asymptotically, there is no distinction between the two algorithms. For the first layer of the tournament, we perform n/2 comparisons, then n/4 for the next, n/8 for the next, and so on. Thus our heapify requires about n-1 comparisons. We then perform n extractions, performing log(n) sift-down steps each time. Both algorithms guarantee O(n + nlog(n)) = O(nlog(n)) time complexity in the worst case. In both algorithms, each element must pass through the root of the tree which bounds their best cases also to O(nlog(n)). Of course, tournament sort's linear spatial complexity and significant overhead make it a poor contender. There is another, however...
Smooth Sort
While searching for algorithms to add to my horde, I naturally stumbled on smooth sort. I was immediately fascinated by it's seemingly magical ability to move elements exactly where they needed to be. It is certainly not easy to understand what is occurring with the gif alone...
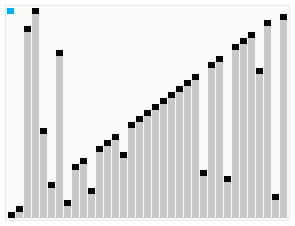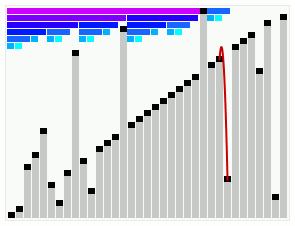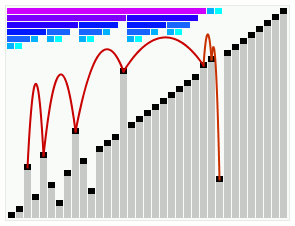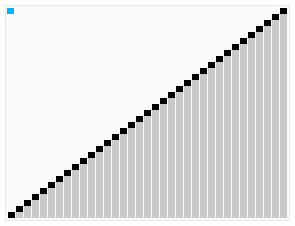
As it happens, smooth sort is particularly useful on nearly-sorted arrays. It trails closely behind bubble sort on sorted arrays, and closely behind heap sort on totally shuffled arrays - at least in theory. As you might've imagined, this algorithm seemed destined to become yet another one of those things that was just out of my reach. It was invented by Dijkstra, who utilized a forest of tree structures - novel tree structures - to obtain this result.
Luckily, this did not turn out to be the case. A great writeup by Keith Schwarz illuminates the subject very well, and I will only summarize the implementation here. As Dijkstra's paper states out its outset, "some, however, consider it a disadvantage of heapsort that it absolutely fails to exploit the circumstances in which the sequence is initially nearly sorted."
That is, heapsort's heapify will completely wreck an already-sorted array only to re-sort it. It will also order the elements in reverse during the construction phase. This is for a simple reason, because if the root of the tree ends up in its final position and it is extracted, then we are left with two separate trees which must be merged. This would occur n times, and the overall result would not be any faster than regular heap sort.
Dijkstra uses a different kind of binary tree with a different kind of implicit representation, however. Schwarz calls this kind of tree a Leonardo Tree, because it always has a number of nodes equal to a Leonardo number, which is any value in the sequence L(0) = 1, L(1) = 1, L(n) = L(n-2) + L(n-1) + 1. The sequence goes 1, 1, 3, 5, 9, 15, 25, etc. It is quite similar to the Fibonacci sequence. You may notice that by combining two such trees whose sizes are consecutive Leonardo numbers with a root, the resulting tree's size is the next Leonardo number.
For our purposes, we will say that Leonardo tree Lt(n) has a left child of Lt(n-1) and a right child of Lt(n-2). So we can combine Lt(3) (size 5) with Lt(2) (size 3) by adding a root to get Lt(4) (size 9).
Critically, it can be shown that any natural number can be expressed as the sum of some Leonardo numbers. This is vital. Schwarz provides a rigorous inductive proof, but I find that the intuition will come easiest through a game you can play in a notepad document, with pen and paper, or anything of the sort. The steps go like this:
You start with an empty list.
- If the list ends with two consecutive Leonardo numbers, replace the pair with their sum plus 1 (the next Leonardo number).
- Otherwise, append 1 to the list.
- Repeat forever!
Note that the duo 1, 1 is a pair of consecutive Leonardo numbers (Lt(1) and Lt(0)). There are three things to notice while playing:
- Regardless of which step you take, you are adding 1 to the sum of the list.
- The list is always in decreasing order.
- When you merge two values, the game starts anew, except that some Leonardo number has been appended to a prefix to the list. This means the game must go on forever.
The third point deserves some explanation. Say you have reached the point where your list consists of only the number 15. In order to have arrived at 15, you first must have arrived at 9. Because you are now effectively playing the game all over again but with 15 prefixed to the list, you will inevitably reach 9 again. Furthermore, once you do, 15 and 9 will be the only elements in the list. If they aren't, then there must be something in between 15 and 9. However, no such Leonardo number exists. There can be no third element after 9, because the previous step must have been to create 9 by merging the last two elements in the list. Therefore, the next step will be to merge 15 and 9 into 25, and 25 will then be the only element in the list. This argument can be applied again, and indefinitely.
We have created a 1-to-1 correspondence between all possible decreasing sequences of Leonardo numbers and natural numbers. Why is this so important? Because it means that any list of values can be encoded in a forest of Leonardo trees of decreasing size. In fact, the crux of the first half of smooth sort is exactly the game described above. (and the crux of the latter half of the algorithm is just playing it, but backwards.) Also, you might notice that each possible natural number corresponds to a specific, distinct decreasing sequence of Leonardo numbers. In other words, the exact shape of the forest is implied by its size. That is the key to smoothsort's O(1) space complexity.
You will also notice that the sequence readily shrinks. Like the Fibonacci sequence, the Leonardo sequence grows exponentially. This means that the maximum number of trees in our forest grows with the log of n. If you played the game for 1,000,000,000 steps, the sequence would never exceed 22 numbers. For this reason, O(1) spatial complexity smoothsort does not really represent an improvement over O(log(n)) spatial complexity smoothsort. If I'm sorting 1 billion 32-bit integers, then I can spare 22 more. For my part, I use a static array with a fixed size of 100. This works for all inputs of size not exceeding about 1.854 sextillion, which I bet will be enough. It exceeds the addressable range of a 64-bit machine by about 2 orders of magnitude. For a 128-bit machine, you'll need an array of size 183.
We start with a list of elements, and we insert elements into the forest. When we do, if the left two trees are consecutive Leonardo numbers, then the inserted element becomes the root of both of them. This is the "merge step" of the game. Otherwise, the node becomes its own tree, the "append 1" step.
We want the root nodes to be sorted, and of course we want the trees to be heapified. All of this allows for sift-down to do its work when we begin extracting elements. The trick is to check whether the root node to the left is larger than both the inserted node and the inserted node's children, if it has any. If it is, we can swap them. The right-most tree will remain heapified if its children were already. If it isn't, we can just sift-down the right-most tree. Since at least one of the children is larger than the root node of the tree to the left, the sorted status of the root nodes will be maintained. If we did do a swap, we repeat the process on the tree to the left and its left neighbor, effectively performing a modified insertion sort.
By the way, if the nodes happen to be inserted in sorted order, then none of this will occur. The nodes will each be inserted into the correct location in O(1) time. If they are in reverse order, then they will be insertion-sorted to the back in about log(n) swaps, and sifted-down the largest Leonardo tree in log(n) recursive calls. In either case, n insertions will occur, for a best case of O(n) and a worst case of O(n(log(n) + log(n))) = O(nlog(n)). The more unsorted the elements, the farther they tend to travel and the more sift-down steps they take. This smooth transition from O(n) best-case to O(nlog(n)) worst-case is the origin of the algorithm's name. The process is mirrored during the extraction phase.
Speaking of the extraction phase, it does not result in moving the element, of course, because the whole idea was to not have to do that. It does, however, orphan two nodes which may have ruined our sorted-roots property. To fix this, we first apply our modified insertion sort to the left node, and then to the right node.
The only thing left now is to define an implicit way of representing these trees in the array. The technique used by Dijkstra was a depth-first, post-order traversal. This means that each node is preceded by its right child. The left child precedes the right child and its descendants. Because we know the number of descendants in the tree rooted at the right child (Its size is always the Leonardo number twice preceding the size of the tree rooted at its parent in the sequence) we can calculate the position of both children in constant time, as with a typical heap.
If the root is at position i, and represents a Leonardo tree Lt(n), then:
- The right child is at position i - 1.
- The left child is at position i - Lt(n-2)
Smooth Sort Visualizer
I've created this simulator to demonstrate the process of constructing and extracting from the Leonardo forest. Nodes connected by a red line are being compared. Along the bottom, you can see the sizes of the highest-order trees in the forest and watch how they change as elements are added and removed. If you queue a few elements and then dequeue them, they will all be in ascending order. I hope it is clear from this how the trees are laid out in memory, and the reason we perform our modified insertion sort when sifting left. Note how, after a dequeue, the orphaned nodes are sifted left.
As for the root nodes of each Leonardo tree in the forest, we can store their positions and sizes in auxiliary arrays of O(lg(n)) size (or a bit vector of size O(1), though the practical improvement is minimal). For my Java implementation, I store only the indices of each tree's size in the Leonardo sequence. This results in undue overhead as the implementation has to repeatedly re-calculate the nth Leonardo number every time it needs one (there is no caching).
For comparison, here are videos of heap sort and smooth sort operating on a shuffled, nearly-sorted, and sorted lists. Note that the times do not stay in sync. Please note also that neither are considered optimal implementations, and the timers do not account for differences in the overhead of recording the logs necessary to generate these videos. This is not a benchmark. Rather, these highlight the functional differences between heap sort and smooth sort.
A later implementation I made in C++ will benchmark my implementations. I am not posting the results because they contain outliers and are not consistent between runs, due presumably to fluctuations in CPU usage. I specifically focused on performance for these. Smooth sort and heap sort were close in time until I switched to an iterative rather than recursive implementation of heap sort, at which point it pulled ahead. Of course, smooth sort will always retain its lead on nearly-sorted data. However, unless you have some reason to assume that the list is in nearly sorted order, heap sort will take less time simply by virtue of the reduced overhead.
This has been a wild project, and it went completely off track literally like four times. Next time, I'm doing block sort. I imagine it'll be worse.