Cubic Spline Interpolation
Let's say you have some points and you'd like to find a function, perhaps even a twice-differentiable function, that passes through those points. Many techniques exist for this purpose, all of which have their own problems. Bezier curves for example are difficult to make twice-differentiable and can loop back on themselves and thus may not actually be functions. Higher-degree polynomials may produce undesirable oscillations referred to as Runge's Phenomenon, Often, the best choice for the job is a cubic spline.
Of course, there is no shortage of libraries and tools to perform these interpolations. In that case you might wonder why I, indeed why anyone, would go through the trouble of implementing a cubic spline interpolation tool from scratch? Isn't it enough simply to have a tentative understanding of the process? The answer is simple: No. I'm a masochist.
This technique is documented very scarcely online, usually in very technical terms, and seemingly never from a programmer's perspective. This is because it is far more complicated than one might expect, and when running into problems requiring this sort of interpolation it is easy to hit a brick wall immediately. For that reason, this guide will go down a number of rabbit holes to explore the underlying topics thoroughly. Many of these can be skipped by anyone who is familiar with the topic.
An Intuitive Definition of a Cubic Spline
A cubic spline is a sequence of cubic functions strung together to form a single smooth line passing through a specified set of points. A cubic function takes the form:
$$y = ax^3 + bx^2 + cx + d$$
Where the coefficients \(a\), \(b\), \(c\), and \(d\) are given constants and \(a \ne 0\). In a spline connecting a sequence of points, each pair of adjacent points is connected by a segment of a cubic function. The entire function itself is therefore a piecewise function consisting of many parts. Each segment is of course restricted in that it must connect the two points that it is defined between. However, we also want each segment to flow smoothly into the next. So the instantaneous rate of change (the slope) at the end of each segment must equal the slope at the beginning of the next segment. In addition to restricting the slope, we also restrict the rate of change of the slope in the same way. If you also define the rate of change of the slope for the first and last points in the sequence (a decision we can make arbitrarily), then we have sufficiently restricted the functions so that we are guaranteed a single solution.
The equations which represent these restrictions form a system of equations which, when solved, produce a list of coefficients for the cubic equations with the properties that we want.
A Technical Definition of a Cubic Spline
We start with a sequence of \(n\) points \((x_1, y_1), (x_2, y_2), (x_3, y_3), \cdots, (x_n, y_n)\). These points must be in order from lowest to highest \(x\) value and no two \(x\) values may be the same: \(x_1 < x_2 < x_3 < \cdots < x_n\).
For each pair of adjacent points \((x_i, y_i), (x_{i+1}, y_{i+1})\) are connected by a cubic \(C_i(x)\) for all \(0 < i < n\), so:
$$C_i(x_i) = y_i$$
$$C_i(x_{i+1}) = y_{i+1}$$
This alone is enough to ensure that the spline forms one continuous line passing through our points. However, there is no guarantee that the spline will be differentiable (smooth). We must add the additional restriction that the slope of two adjacent segments is the same where one ends and the next begins, which is the same as saying that the values of the derivatives are equal at that point:
$$C_i'(x_{i+1}) = C_{i+1}'(x_{i+1})$$
And we add the same restriction to their second derivatives:
$$C_i''(x_{i+1}) = C_{i+1}''(x_{i+1})$$
These two restrictions apply for all \(0 < i < n - 1\), meaning they do not restrict the slope at the first or last points in the sequence. We must do this ourselves and we have any number of options (called "boundary conditions") to choose from which will be covered later, but the natural choice (it's literally called the "natural" or "simple" boundary condition) is to set the second derivative at the endpoints equal to 0:
$$C_1''(x_1) = 0$$
$$C_{n-1}''(x_n) = 0$$
Finally, we have our spline, defined as a piecewise function, the composition of each cubic section:
$$ S(x) = \left\{ \begin{array}{lr} C_1(x), & \text{if } x_1 \le x < x_2\\ C_2(x), & \text{if } x_2 \le x < x_3\\ C_3(x), & \text{if } x_3 \le x < x_4\\ \cdots\\ C_{n-1}(x), & \text{if } x_{n-1} \le x \le x_n \end{array} \right\} $$
Combined, the above equations form a system of equations which can be solved to find the coefficients of the cubics satisfying these restrictions.
An Aside on Calculus
In a function defined as \(y = f(x)\), the instantaneous rate of change of \(y\) with respect to \(x\) is a very useful thing to be able to find. In essence, it allows one to find the slope of a function at any point, assuming such a slope exists. The derivative of a function, denoted with a tick mark, gives the slope of the function at a particular x value. So, \(f'(x)\) gives the slope of \(f\) at \(x\). Taking the derivative of a polynomial such as a cubic is easy. For each term, simply multiply the term by the exponent and subtract one from the exponent. So the derivative of
$$f(x) = 2x^3 + x^2 - 4x + 3$$
is
$$f'(x) = 6x^2 + 2x - 4$$
which gives the rate of change of \(f(x)\) at any given \(x\). So, if I were to write
$$f'(4) = g'(4)$$
then I'm saying that the functions \(f(x)\) and \(g(x)\) have the same slope at \(x = 4\). We can also derive the above function, producing the second derivative of \(f(x)\)...$$f''(x) = 12x + 2$$
which you might say gives the rate of change of the rate of change of \(f(x)\) at any given \(x\). These techniques are only applicable to functions which are both differentiable and continuous, which all polynomials are. These are in essence formalizations of the concept of "smoothness" as it applies to functions. When we apply restrictions to the derivatives of the cubics which compose the spline, we are ensuring the the rate of change of \(x\) with respect to \(y\) does not change rapidly between adjacent segments, and therefore we are ensuring that the resulting spline is actually smooth.Producing the System of Equations
First, please recall the equations from the technical definition:
\(C_i(x_i) = y_i, \text{ } 0 < i < n\)
\(C_i(x_{i+1}) = y_{i+1}, \text{ } 0 < i < n\)
\(C_i'(x_{i+1}) = C_{i+1}'(x_{i+1}), \text{ } 0 < i < n - 1\)
\(C_i''(x_{i+1}) = C_{i+1}''(x_{i+1}), \text{ } 0 < i < n - 1\)
\(C_1''(x_1) = 0\)
\(C_{n-1}''(x_n) = 0\)
In order to produce the system of equations, we must expand out our restrictions into their final forms. For this, we'll use a simple example consisting of only four points:
$$(1, 2),\text{ }(2, 4),\text{ }(4, 3),\text{ }(5, 1)$$
This process will produce 12 equations. I'll begin by applying the first two equations, restricting the cubics to pass through the specified points. We do this by first enumerating the equation for each \(0 < i < n\), writing them out in cubic form, and substituting the appropriate \(x\) and \(y\) values from our sequence of points.
$$a_1 + b_1 + c_1 + d_1 = 2$$
$$8a_1 + 4b_1 + 2c_1 + d_1 = 4$$
$$8a_2 + 4b_2 + 2c_2 + d_2 = 4$$
$$64a_2 + 14b_2 + 4c_2 + d_2 = 3$$
$$64a_3 + 14b_3 + 4c_3 + d_3 = 3$$
$$125a_3 + 25b_3 + 5_c3 + d_3 = 1$$
Then I'll apply the third equation for each \(0 < i < n - 1\)...
$$12a_1 + 4b_1 + c_1 = 12a_2 + 4b_2 + c_2$$
$$48a_2 + 8b_2 + c_2 = 48a_3 + 8b_3 + c_3$$
And the fourth equation as well, ensuring the spline will be twice differentiable...
$$12a_1 + 2b_1 = 12a_2 + 2b_2$$
$$24a_2 + 2b_2 = 24a_3 + 2b_3$$
Finally, we apply the last two equations which define the slope of our spline at the first and last point.
$$6a_1 + 2b_1 = 0$$
$$30a_3 + 2b_3 = 0$$
And that's our system of equations! Now we only have... 12 coefficients to solve for. Yeah, solving systems of equations like this by substitution is something I imagine I'll be tasked with after I'm inevitably consigned to eternal hellfire. Thankfully, there's a better way.
A Brief Introduction to Matrices
A matrix is a sequence of vectors. Matrix multiplication involves producing a matrix from the dot products of the components of the vectors composing the multiplicands. To clarify, I'll start with the dot product. For the unfamiliar, this is the sum of the products of the corresponding elements in each vector. For example, consider the following two vectors:
$$ \left[ \begin{array}{lr} 2\\ 6\\ 3 \end{array} \right] \cdot \left[ \begin{array}{lr} 1\\ 4\\ 7 \end{array} \right] $$
To find the dot product, we multiply the first pair of elements to get 2. We then add that to the product of the middle elements to get a total of 26, and finally we add the product of the bottom elements to get a total 47. This pattern repeats for longer vectors. The \(\cdot\) symbol indicates the dot product, whereas the \(\times\) symbol indicates the cross product, another operation which isn't important for solving our problem.
When we multiply matrices, we take the dot product of each row in the first matrix and each column in the second matrix. The result goes in the same row and column as the arguments that we took the dot product of. Consider the following example:
$$ \left[ \begin{array}{lr} 2 & 3 & 1\\ 4 & 6 & 4\\ 3 & 2 & 7 \end{array} \right] \cdot \left[ \begin{array}{lr} 1 & 2 & 2\\ 3 & 5 & 4\\ 6 & 6 & 8 \end{array} \right] = \left[ \begin{array}{lr} \_ & \_ & \_\\ \_ & \_ & \_\\ \_ & \_ & \_ \end{array} \right] $$
The upper-left element of the product will be the dot product of the upper row from the first matrix and the left column from the second matrix.
$$ \left[ \begin{array}{lr} 2\\ 3\\ 1 \end{array} \right] \cdot \left[ \begin{array}{lr} 1\\ 3\\ 6 \end{array} \right] = 2\cdot1 + 3\cdot3 + 1\cdot6 = 17 $$
$$ \left[ \begin{array}{lr} \underline2 & \underline3 & \underline1\\ 4 & 6 & 4\\ 3 & 2 & 7 \end{array} \right] \cdot \left[ \begin{array}{lr} \underline1 & 2 & 2\\ \underline3 & 5 & 4\\ \underline6 & 6 & 8 \end{array} \right] = \left[ \begin{array}{lr} 17 & \_ & \_\\ \_ & \_ & \_\\ \_ & \_ & \_ \end{array} \right] $$
Similarly, the middle right element will take the middle row and right column...
$$ \left[ \begin{array}{lr} 4\\ 6\\ 4 \end{array} \right] \cdot \left[ \begin{array}{lr} 2\\ 4\\ 8 \end{array} \right] = 2\cdot4 + 6\cdot4 + 4\cdot8 = 64 $$
$$ \left[ \begin{array}{lr} 2 & 3 & 1\\ \underline4 & \underline6 & \underline4\\ 3 & 2 & 7 \end{array} \right] \cdot \left[ \begin{array}{lr} 1 & 2 & \underline2\\ 3 & 5 & \underline4\\ 6 & 6 & \underline8 \end{array} \right] = \left[ \begin{array}{lr} 17 & \_ & \_\\ \_ & \_ & 64\\ \_ & \_ & \_ \end{array} \right] $$
The middle element takes the middle row and middle column...
$$ \left[ \begin{array}{lr} 4\\ 6\\ 4 \end{array} \right] \cdot \left[ \begin{array}{lr} 2\\ 5\\ 6 \end{array} \right] = 4\cdot2 + 6\cdot5 + 4\cdot6 = 62 $$
$$ \left[ \begin{array}{lr} 2 & 3 & 1\\ \underline4 & \underline6 & \underline4\\ 3 & 2 & 7 \end{array} \right] \cdot \left[ \begin{array}{lr} 1 & \underline2 & 2\\ 3 & \underline5 & 4\\ 6 & \underline6 & 8 \end{array} \right] = \left[ \begin{array}{lr} 17 & \_ & \_\\ \_ & 62 & 64\\ \_ & \_ & \_ \end{array} \right] $$
And so on for all the rows and columns.$$ \left[ \begin{array}{lr} 2 & 3 & 1\\ 4 & 6 & 4\\ 3 & 2 & 7 \end{array} \right] \cdot \left[ \begin{array}{lr} 1 & 2 & 2\\ 3 & 5 & 4\\ 6 & 6 & 8 \end{array} \right] = \left[ \begin{array}{lr} 17 & 25 & 24\\ 46 & 62 & 64\\ 51 & 58 & 70 \end{array} \right] $$
Of course, you can compute them in any order. The matrices do not have to be squares, as long as the second matrix has as many rows as the first has columns, because otherwise the dot product can't be computed. Matrix multiplication is associative, but not commutative! So, when attaining the product of multiple matrices, you may perform the operations in any order. However, you may not swap the order of the multiplicands in a multiplication. For matrices, \(A\times B \ne B\times A\).
Solving Systems of Equations
So, why is it that I've even taken the time to discuss matrix multiplication? The reason is that matrices happen to be particularly useful when it comes to representing and solving systems of equations. Consider the following equations:
$$-2a + 7b + 6c = 43$$
$$-6a - 4b + 3c = 4$$
$$5b + 2c = 20$$
Of course, we could solve these equations through substitution, though I've tried to make such a process painful. So, instead, lets try to solve it with matrix multiplication. You might think of the equations as representing dot products. After all, they are just sums of products. For example, the first equation could be represented as
$$ \left[ \begin{array}{lr} -2\\ 7\\ 6\\ \end{array} \right] \cdot \left[ \begin{array}{lr} a\\ b\\ c \end{array} \right] = 43 $$
and the last could be represented as
$$ \left[ \begin{array}{lr} 0\\ 5\\ 2 \end{array} \right] \cdot \left[ \begin{array}{lr} a\\ b\\ c \end{array} \right] = 20 $$
In fact, we could show the entire system of equations as a matrix multiplication.
$$ \left[ \begin{array}{lr} -2 & 7 & 6\\ -6 & -4 & 3\\ 0 & 5 & 2 \end{array} \right] \cdot \left[ \begin{array}{lr} a\\ b\\ c \end{array} \right] = \left[ \begin{array}{lr} 43\\ 4\\ 20 \end{array} \right] $$
Writing out the dot products in such a multiplication gives back the original equations. If we write out the equation using letters to represent the matrices, we get
$$AX = B$$
and it doesn't get much simpler than that. We could simply multiply both sides by the inverse of \(A\), which we write as \(A^{-1}\). The inverse of a matrix is a lot like the reciprocal of a scalar value. Multiplying a matrix by its inverse gives the identity matrix, which is a lot like the number 1 in that multiplying anything by the identity matrix leaves it unchanged.
$$X = A^{-1}B$$
$$ A^{-1} = \left[ \begin{array}{lr} -2 & 7 & 6\\ -6 & -4 & 3\\ 0 & 5 & 2 \end{array} \right]^{-1} = \left[ \begin{array}{lr} 0.46 & -0.32 & -0.9\\ -0.24 & 0.08 & 0.6\\ 0.6 & -0.2 & -1 \end{array} \right] $$
$$ \left[ \begin{array}{lr} a\\ b\\ c \end{array} \right] = \left[ \begin{array}{lr} 0.46 & -0.32 & -0.9\\ -0.24 & 0.08 & 0.6\\ 0.6 & -0.2 & -1 \end{array} \right] \cdot \left[ \begin{array}{lr} 43\\ 4\\ 20 \end{array} \right] = \left[ \begin{array}{lr} 0.5\\ 2\\ 5 \end{array} \right] $$
And there's our solution, \(a=0.5\), \(b=2\), \(c=5\). There's a problem, however. You may have noticed that I skipped over the computation of the inverse rather quickly. That's because we won't be using this particular method for solving our system of equations because it requires calculating the determinant of the matrix, which is incredibly computationally expensive unless you use a technique called Gaussian elimination. However, if we use Gaussian elimination, then we won't even need to use the determinant anyways.
Gaussian Elimination
Performing Gaussian elimination puts a matrix into row echelon form, where the bottom-left half of the matrix is all zeroes. A bit more formally, we refer to the left-most non-zero element in a row to be the leading entry. When a matrix is in row echelon form, the leading entry of each row is farther to the left than all of the leading entries beneath it. Put another way, every leading entry in every row of the matrix must have only zeroes beneath it. If a row is empty, it must end up at the bottom of the matrix.
Sometimes, "row echelon form" is given the additional requirement the the leading entry in each row must be 1. For our program, however, we will not have any need to reduce the matrix in this capacity.
In order to perform Gaussian elimination, we may execute any of the following elementary row operations any number of times and in any order:
- Swap two rows.
- Multiply each element of one row by a non-zero scalar.
- Add a scalar multiple of one row to another.
Critically, these operations must also include the elements of the matrix \(B\) as if the elements in that matrix belonged to the rows of matrix \(A\). These operations mimic algebraic operations on the equations that we're representing. For example, multiplying every element in a row by a scalar is the same as multiplying every term in the underlying equation by that scalar. Swapping rows naturally has no effect, because of course our equations have no sense of "order". Adding a scalar multiple of one row to another row can be used to perform substitution. For example, consider the following example matrices:
$$ \left[ \begin{array}{lr} 3 & 4\\ 6 & 2 \end{array} \right] \cdot \left[ \begin{array}{lr} a\\ b \end{array} \right] = \left[ \begin{array}{lr} 29\\ 28 \end{array} \right] $$
Which represents the following equations:
$$3a + 4b = 29$$
$$6a + 2b = 28$$
If we were to add the first row times \(-2\) to the second row, Remembering to also operate on the right-hand side, we'd end up with:
$$ \left[ \begin{array}{lr} 3 & 4\\ 0 & -6 \end{array} \right] \cdot \left[ \begin{array}{lr} a\\ b \end{array} \right] = \left[ \begin{array}{lr} 29\\ -30 \end{array} \right] $$
Which has the same effect solving for \(6a\)
$$3a + 4b = 29$$
$$-6a -8b = -58$$
$$6a = -8b + 58$$
and then performing a substitution:
$$(-8b + 58) + 2b = 28$$
$$-6b = -30$$
The last equation here is what we got in the matrix above. Now, solving the system of equations is trivial by simplifying the equation for \(b\) and substituting it into the first equation.
Programmatically, we would execute this algorithm by iterating over the elements in the matrix's diagonal from the upper left to the lower right. We'll call the element we're currently on \(k\). For each \(k\) we'll iterate over all of the elements beneath it and we'll call the one we're currently on \(i\). For each of these, we'll calculate \(m = -i / k\). Naturally, it follows that \(m \cdot k + i = 0\). We take a copy of the entire row containing \(k\) multiplied by \(m\) and add it to the entire row containing \(i\). Once we complete this for all rows beneath \(k\), all the entries beneath \(k\) will be \(0\). Once we've gone down the entire diagonal, the matrix will be in row echelon form.
As an example, we'll perform this process on our example matrix from before.
$$ \left[ \begin{array}{lr} -2 & 7 & 6\\ -6 & -4 & 3\\ 0 & 5 & 2 \end{array} \right] \left[ \begin{array}{lr} 43\\ 4\\ 20 \end{array} \right] $$
Our first \(k\) will of course be the upper left entry, \(-2\), and our first \(i\) will be the entry directly beneath it, \(-6\). Therefore, \(m = -i / k = -3\). We multiply the entire top row by \(m\)...
$$ \left[ \begin{array}{lr} -2 & 7 & 6 \end{array} \right] \left[ \begin{array}{lr} 43 \end{array} \right] \cdot -3 = \left[ \begin{array}{lr} 6 & -21 & -18 \end{array} \right] \left[ \begin{array}{lr} -129 \end{array} \right] $$
And add that into the second row...
$$ \left[ \begin{array}{lr} -6 & -4 & 3 \end{array} \right] \left[ \begin{array}{lr} 4 \end{array} \right] + \left[ \begin{array}{lr} 6 & -21 & -18 \end{array} \right] \left[ \begin{array}{lr} -129 \end{array} \right] = \left[ \begin{array}{lr} 0 & -25 & -15 \end{array} \right] \left[ \begin{array}{lr} -125 \end{array} \right] $$
So that our matrix becomes
$$ \left[ \begin{array}{lr} -2 & 7 & 6\\ 0 & -25 & -15\\ 0 & 5 & 2 \end{array} \right] \left[ \begin{array}{lr} 43\\ -125\\ 20 \end{array} \right] $$
Then we do the same thing with the next \(i\). \(i\) is 0 here already, so we get to skip it. If you were to go through the process, you would end up adding all 0's to the third row. Our next \(k\) is the very middle element, \(-25\), and our next \(i\) is the one beneath it, \(5\). \(m = -5 / -25 = \frac{1}{5}\). We multiply the second row by \(m\) to get
$$ \left[ \begin{array}{lr} 0 & -25 & -15\\ \end{array} \right] \left[ \begin{array}{lr} -125\\ \end{array} \right] \cdot \frac{1}{5} = \left[ \begin{array}{lr} 0 & -5 & -3 \end{array} \right] \left[ \begin{array}{lr} -25 \end{array} \right] $$
and add that back in to the last row, giving us our matrix in row echelon form:
$$ \left[ \begin{array}{lr} -2 & 7 & 6\\ 0 & -25 & -15\\ 0 & 0 & -1 \end{array} \right] \left[ \begin{array}{lr} a\\ b\\ c \end{array} \right] = \left[ \begin{array}{lr} 43\\ -125\\ -5 \end{array} \right] $$
And this is where the magic happens. If we convert the matrices back into equations...
$$-2a + 7b + 6c = 43$$
$$-25b - 15c = -125$$
$$-c = -5$$
then suddenly the solution is very easy! Clearly, \(c = 5\), therefore...
$$-25b - 15(5) = -125$$
$$-5b - 15 = -25$$
$$b=2$$
and finally...
$$-2a + 7(2) + 6(5) = 43$$
$$-2a + 44 = 43$$
$$a = 0.5$$
And there we have our solutions. I know I skipped over matrix inversion so some may not recognize this, but trust me, we bypassed a lot of hassle with that. Using Gaussian elimination, we now how a much simpler, faster, and more scalable technique for solving systems of equations than we could ever achieve otherwise. Recall for a moment that the simplest possible spline between two points (remember, that's what we're doing?) would have 8 equations and as many unknowns.
There is one small issue, however. If \(k\) is ever \(0\), then this algorithm will perform a division by \(0\). At first I figured you could just find a row for which this element isn't \(0\) and swap the two, but there's a slightly cleverer way to handle this that I stole from GeeksForGeeks. The trick is to preemptively iterate over all the values for \(i\) and find the largest, then swap it with the row containing \(k\). This probably also reduces the severity of floating point errors by ensuring that the products are more reasonably sized and whatnot. If the largest possible \(i\) is \(0\), then the system of equations either has infinitely many solutions or no solutions. I'm pretty sure that'll never happen for the particular program that we're building, but just in case it does, I'll makes sure not to handle the error so the program crashes and then I'll know for certain.
In any case, the computer isn't going to convert the matrices back to equation form, it'll hold onto the equations in matrix form from start to finish. So, how do we solve them without things getting too complicated? Firstly, we'll solve for the unknowns from the bottom to the top. This is how we naturally solved them previously, and that has to do with the nature of the matrix after Gaussian elimination (although the algorithm can be performed so that it has all the zeroes in the upper right instead, allowing the unknowns to be solved from top to bottom). Clearly, the unknown on the very bottom can be found through a simple division.
$$ \left[ \begin{array}{lr} -2 & 7 & 6\\ 0 & -25 & -15\\ 0 & 0 & -1 \end{array} \right] \left[ \begin{array}{lr} a\\ b\\ c \end{array} \right] = \left[ \begin{array}{lr} 43\\ -125\\ -5 \end{array} \right] $$
$$ \left[ \begin{array}{lr} 0\\ 0\\ -1 \end{array} \right] \cdot \left[ \begin{array}{lr} a\\ b\\ c \end{array} \right] = 0 \cdot a + 0 \cdot b - 1 \cdot c = -5 $$
However, the next unknown requires a subtraction followed by another division.
$$ \left[ \begin{array}{lr} 0\\ -25\\ -15 \end{array} \right] \cdot \left[ \begin{array}{lr} a\\ b\\ c \end{array} \right] = 0 \cdot a + -25 \cdot b - 15 \cdot 5 = -125 $$
And for the final unknown you perform two subtractions followed by a division.
$$ \left[ \begin{array}{lr} -2\\ 7\\ 6 \end{array} \right] \cdot \left[ \begin{array}{lr} a\\ b\\ c \end{array} \right] = -2 \cdot a + 7 \cdot 2 + 6 \cdot 5 = 43 $$
With a little thought about the nature of row echelon form, one might come to realize that this pattern must always occur, and must always be the case as long as the matrix is square. Therefore, the solution can be found by taking all of the entries in a row except the leading entry (assuming they exist) and multiplying them by the corresponding value on the right-hand side. The sum of these products is subtracted from the value on the right hand side which corresponds to the leading entry for the row you're evaluating. Once you've done that, you can divide the remaining value on the right-hand side by the leading entry for that row to get the final coefficient. You might write these equations like so:
$$c = -5 / -1$$
$$b = (-125 - (-15)c) / -25$$
$$a = (43 - 7b - 6c) / -2$$
And that's the entire algorithm. Using all of this combined, we should now be able to write the necessary functions to solve for the coefficients of the cubics connecting any arbitrary set of points.
Loading the Matrix
Loading the matrix is a somewhat more complex task here than it was in the example. Firstly, we have our restrictive equations given below.
\(C_i(x_i) = y_i, \text{ } 0 < i < n\)
\(C_i(x_{i+1}) = y_{i+1}, \text{ } 0 < i < n\)
\(C_i'(x_{i+1}) = C_{i+1}'(x_{i+1}), \text{ } 0 < i < n - 1\)
\(C_i''(x_{i+1}) = C_{i+1}''(x_{i+1}), \text{ } 0 < i < n - 1\)
\(C_1''(x_1) = 0\)
\(C_{n-1}''(x_n) = 0\)
We just need to write each of the functions out in cubic form. We'll also move the right-hand side of the middle equations over so that they are equal to zero. It's important that all of the unknowns are on the left side of the equation.
\(a_ix_i^3 + b_ix_i^2 + c_ix + d_i = y_i\)
\(a_ix_{i+1}^3 + b_ix_{i+1}^2 + c_ix_{i+1} + d_i = y_{i+1}\)
\(3a_ix_{i+1}^2 + 2b_ix_{i+1} + c_i - 3a_{i+1}x_{i+1}^2 - 2b_{i+1}x_{i+1} - c_{i+1} = 0\)
\(6a_ix_{i+1} + 2b_i - 6a_{i+1}x_{i+1} - 2b_{i+1} = 0\)
\(6a_1x_1 + 2b_1 = 0\)
\(6a_{n-1}x_n - 2b_{n-1} = 0\)
If we recall the ranges of \(i\) for which these functions are each valid, we'll see that there are \(n-1\) variants of the top two equations, \(n-2\) variants of the middle equations, and only \(1\) variant for each of the bottom two equations. The total number of equations we'll generate is therefore \(2(n-1) + 2(n-2) + 2 = 4n-4\), which becomes the width and height of the matrix we'd like to create. Although we'll give the matrix an additional column to hold the \(B\) matrix with the right-hand side of our equations. Aside from this extra column, it is a rule that solving a system of equations like this will utilize a square matrix.
Previously, we found a system of equations by enumerating the variants of each of the above equations for each valid value of \(i\). Then, we substituted in the \(x\) and \(y\) values from the input points into those equations to produce the following system. We used the points \((1, 2)\), \((2, 4)\), \((4, 3)\), \((5, 1)\). In this case, \(n=4\), and as you can see the process did indeed give rise to \(4n-4 = 12\) equations.
$$a_1 + b_1 + c_1 + d_1 = 2$$
$$8a_1 + 4b_1 + 2c_1 + d_1 = 4$$
$$8a_2 + 4b_2 + 2c_2 + d_2 = 4$$
$$64a_2 + 14b_2 + 4c_2 + d_2 = 3$$
$$64a_3 + 14b_3 + 4c_3 + d_3 = 3$$
$$125a_3 + 25b_3 + 5c_3 + d_3 = 1$$
$$12a_1 + 4b_1 + c_1 = 12a_2 + 4b_2 + c_2$$
$$48a_2 + 8b_2 + c_2 = 48a_3 + 8b_3 + c_3$$
$$12a_1 + 2b_1 = 12a_2 + 2b_2$$
$$24a_2 + 2b_2 = 24a_3 + 2b_3$$
$$6a_1 + 2b_1 = 0$$
$$30a_3 + 2b_3 = 0$$
We can rewrite these equations to move all the unknowns to the left hand side, and so that they each include all of the unknowns in the entire system, which are all multiplied by 0.
$$1a_1 + 1b_1 + 1c_1 +1 d_1 + 0a_2 + 0b_2 + 0c_2 + 0d_2 + 0a_3 + 0b_3 + 0c_3 + 0d_3 = 2$$
$$8a_1 + 4b_1 + 2c_1 + 1d_1 + 0a_2 + 0b_2 + 0c_2 + 0d_2 + 0a_3 + 0b_3 + 0c_3 + 0d_3 = 4$$
$$0a_1 + 0b_1 + 0c_1 + 0d_1 + 8a_2 + 4b_2 + 2c_2 + 1d_2 + 0a_3 + 0b_3 + 0c_3 + 0d_3 = 4$$
$$0a_1 + 0b_1 + 0c_1 + 0d_1 + 64a_2 + 14b_2 + 4c_2 + 1d_2 + 0a_3 + 0b_3 + 0c_3 + 0d_3 = 3$$
$$0a_1 + 0b_1 + 0c_1 + 0d_1 + 0a_2 + 0b_2 + 0c_2 + 0d_2 + 64a_3 + 14b_3 + 4c_3 + 1d_3 = 3$$
$$0a_1 + 0b_1 + 0c_1 + 0d_1 + 0a_2 + 0b_2 + 0c_2 + 0d_2 + 125a_3 + 25b_3 + 5c_3 + 1d_3 = 1$$
$$12a_1 + 4b_1 + 1c_1 + 0d_1 - 12a_2 - 4b_2 - 1c_2 + 0d_2 + 0a_3 + 0b_3 + 0c_3 + 0d_3 = 0$$
$$0a_1 + 0b_1 + 0c_1 + 0d_1 + 48a_2 + 8b_2 + 1c_2 + 0d_2 - 48a_3 - 8b_3 - 1c_3 + 0d_3 = 0$$
$$12a_1 + 2b_1 + 0c_1 + 0d_1 - 12a_2 - 2b_2 + 0c_2 + 0d_2 + 0a_3 + 0b_3 + 0c_3 + 0d_3 = 0$$
$$0a_1 + 0b_1 + 0c_1 + 0d_1 + 24a_2 + 2b_2 + 0c_2 + 0d_2- 24a_3 - 2b_3 + 0c_3 + 0d_3 = 0$$
$$6a_1 + 2b_1 + 0c_1 + 0d_1 + 0a_2 + 0b_2 + 0c_2 + 0d_2 + 0a_3 + 0b_3 + 0c_3 + 0d_3 = 0$$
$$0a_1 + 0b_1 + 0c_1 + 0d_1 + 0a_2 + 0b_2 + 0c_2 + 0d_2 + 30a_3 + 2b_3 + 0c_3 + 0d_3 = 0$$
And hopefully, despite the perhaps slightly terrifying-looking nature of these equations, it's clear how we'll load these into the matrix. After all, they're already in the precise arrangement that we need. The matrix form of these equations is given below.
$$ \left[ \begin{array}{lr} 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 8 & 4 & 2 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 8 & 4 & 2 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 64 & 14 & 4 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 64 & 14 & 4 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 &125 & 25 & 5 & 1 \\ 12 & 4 & 1 & 0 &-12 & -4 & -1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 48 & 8 & 1 & 0 &-48 & -8 & -1 & 0 \\ 12 & 2 & 0 & 0 &-12 & -2 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 24 & 2 & 0 & 0 &-24 & -2 & 0 & 0 \\ 6 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 30 & 2 & 0 & 0 \end{array} \right] \cdot \left[ \begin{array}{lr} a_1 \\ b_1 \\ c_1 \\ d_1 \\ a_2 \\ b_2 \\ c_2 \\ d_2 \\ a_3 \\ b_3 \\ c_3 \\ d_3 \end{array} \right] = \left[ \begin{array}{lr} 2 \\ 4 \\ 4 \\ 3 \\ 3 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} \right] $$
Now we can proceed with Gaussian elimination and backwards substitution, which have already been described, to solve for the coefficients we need.
Writing the Program
I'll be writing the program in C. The final program came out to be 203 lines and starts with the matrix generation. I start by allocating the space for the matrix. Then, I split the points array into individual arrays for the \(x\) and \(y\) components for code readability. Finally, I cache the squares and cubes of all of the x values which improves readability (in my opinion) and also reduces the number of multiplications needed.
For clarity:
X[i]= \(x_i\)Y[i]= \(y_i\)squares[i]= \(x_i^2\)cubes[i]= \(x_i^3\)num_points= \(n\)N= \(4n-4\)
// Accepts the list of num_points points as an array of 2*num_points doubles.
// points[2*i] = x_i, points[2*i+1] = y_i
double** generate_matrix(double* points, int num_points) {
int N = num_points * 4 - 4;
// Allocate matrix. Add and extra column for the RHS.
double** mat = (double**) malloc(sizeof(double*) * N);
for (int i = 0; i < N; i++) {
mat[i] = malloc(sizeof(double) * (N+1));
for (int j = 0; j <= N; j++) {
mat[i][j] = 0;
}
}
// Split the x and y values into separate arrays, which makes the array accesses a bit simpler down the line.
double X[num_points];
double Y[num_points];
for (int i = 0; i < num_points; i++) {
X[i] = points[i*2];
Y[i] = points[i*2+1];
}
// Initialize matrix.
// Calculate and cache the squares and cubes of each of the x values.
double squares[num_points];
double cubes[num_points];
for (int i = 0; i < num_points; i++) {
squares[i] = X[i] * X[i];
cubes[i] = X[i] * squares[i];
}
// Code to load the matrix will go here.
}
The next snippet, loading the values into the matrix, is perhaps the most difficult part of the code. We have to write the coefficients for the unknowns into the matrix based on the points passed to the function. To avoid the complications of calculating which row to write each equation to, I simply have the variable r indicate that row and I increment it after each row written.
At this point it's good to note that, because the points and matrix are 0-indexed, the code may be off by one compared to the math done above. For example, the first pair of restrictive equations are now defined for \(0 \le i < n-1\) instead of \(0 < i < n\).
// The row we're currently packing an equation into.
// This will be incremented every time we move to another row.
int r = 0;
// Restrict functions by a pair of points that they must pass through.
for (int i = 0; i < num_points-1; i++) {
// a_i * x_i^3 + b_i * x_i^2 + c_i * x_i + d_i = y_i
mat[r][i*4 ] = cubes[i];
mat[r][i*4+1] = squares[i];
mat[r][i*4+2] = X[i];
mat[r][i*4+3] = 1;
mat[r][N] = Y[i];
r++;
// a_i * x_(i+1)^3 + b_i * x_(i+1)^2 + c_i * x_(i+1) + d_i = y_(i+1)
mat[r][i*4 ] = cubes[i+1];
mat[r][i*4+1] = squares[i+1];
mat[r][i*4+2] = X[i+1];
mat[r][i*4+3] = 1;
mat[r][N] = Y[i+1];
r++;
}
// Restrict adjacent segments to have the same first derivative where they meet.
for (int i = 0; i < num_points-2; i++) {
// 3 * a_i * x_(i+1)^2 + 2 * b_i * x_(i+1) + c_i - 3 * a_(i+1) * x_(i+1)^2 - 2 * b_(i+1) * x_(i+1) - c_(i+1) = 0
mat[r][i*4 ] = 3 * squares[i+1];
mat[r][i*4+1] = 2 * X[i+1];
mat[r][i*4+2] = 1;
mat[r][(i+1)*4 ] = -3 * squares[i+1];
mat[r][(i+1)*4+1] = -2 * X[i+1];
mat[r][(i+1)*4+2] = -1;
r++;
}
// Restrict adjacent segments to have the same second derivative where they meet.
for (int i = 0; i < num_points-2; i++) {
// 6 * a_i * x_(i+1) + 2 * b_i - 6 * a_(i+1) * x_(i+1) - 2 * b_(i+1) = 0;
mat[r][i*4 ] = 6 * X[i+1];
mat[r][i*4+1] = 2;
mat[r][(i+1)*4 ] = -6 * X[i+1];
mat[r][(i+1)*4+1] = -2;
r++;
}
// Restrict the second derivative at the first and last points.
// 6 * a_1 * x_1 + 2 * b_1 = 0
mat[r][0] = 6 * X[0];
mat[r][1] = 2;
r++;
// 6 * a_(n-1) * x_n + 2 * b_(n-1) = 0
mat[r][(num_points-2)*4 ] = 6 * X[num_points-1];
mat[r][(num_points-2)*4+1] = 2;
return mat;
Now we can make a few utility functions. First, we'll definitely need a function to display the state of the matrix at any time. It'll print the values in the matrix and indices along the top. We'll also make a small function for swapping two rows in the matrix. Because I'm working in C, I'll also need to write a function to deallocate the matrix.
void print_matrix(double** mat, int num_points) {
int N = num_points * 4 - 4;
for (int j = 0; j < N; j++) {
printf("%7d ", j);
}
printf("\n");
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
printf("%7.3lf ", mat[i][j]);
}
printf("| %7.3lf\n", mat[i][N]);
}
}
// Swap two rows in the matrix
void swap_rows(double** mat, int i, int j) {
double* temp = mat[i];
mat[i] = mat[j];
mat[j] = temp;
}
void free_matrix(double** mat, int num_points) {
int N = num_points * 4 - 4;
for (int i = 0; i < N; i++) {
free(mat[i]);
}
free(mat);
}
As for the main function, we'll create our list of points and pass it to the generator function and print out its state.
int main() {
double points[] = {0, 2, 1, 8, 4, 4, 5, 4, 7, 6};
int num_points = 5;
double** mat = generate_matrix(points, num_points);
print_matrix(mat, num_points);
free_matrix(mat, num_points);
return 0;
}
If you used the same points and the program is working, your matrix should look like this.
$$ \left[ \begin{array}{lr} 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 64 & 16 & 4 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 64 & 16 & 4 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 &125 & 25 & 5 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 &125 & 25 & 5 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 &343 & 49 & 7 & 1 \\ 3 & 2 & 1 & 0 & -3 & -2 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 48 & 8 & 1 & 0 &-48 & -8 & -1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 75 & 10 & 1 & 0 &-75 &-10 & -1 & 0 \\ 6 & 2 & 0 & 0 & -6 & -2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 24 & 2 & 0 & 0 &-24 & -2 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 30 & 2 & 0 & 0 &-30 & -2 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 42 & 2 & 0 & 0 \end{array} \right] \left[ \begin{array}{lr} 2 \\ 8 \\ 8 \\ 4 \\ 4 \\ 4 \\ 4 \\ 6 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} \right] $$
Next we have the Gaussian elimination process. As discussed previously, we will iterate over the diagonal of the matrix and, for each entry k, we will iterate over the column beneath it. We find which of these entries has the largest absolute value and swap it's row with the row containing k. If the largest entry is 0, then the system either has no solutions or infinitely many solutions, so we can't solve it. We then iterate over each of the values below k again. For each entry i in this column, we multiply the row containing k by m and add the result to the row containing i. m is calculated as \(m = -i / k\). For clarity's sake, I'll mention that multiplying a row by a scalar means multiplying all of its elements by that scalar. To add two rows, we add together all of the corresponding elements in their rows.
We return 1 if the system can't be solved, 0 otherwise. Although there are of course plenty of systems of equations that can't be solved, the matrix generator we've written will never produce an unsolvable set... I think. So if this function ever returns 1, then there is something wrong with the code.
// Perform Gaussian elimination to bring the matrix into row echelon form.
// The matrix is not put into reduced row echelon form.
int gaussian_elimination(double** mat, int num_points) {
int N = num_points * 4 - 4;
// Iterate over the diagonal.
for (int k = 0; k < N; k++) {
// Find the largest entry among the entries beneath k.
double max_i = fabs(mat[k][k]);
int max_i_row = k;
for (int i = k+1; i < N; i++) {
if (fabs(mat[i][k]) > max_i) {
max_i = fabs(mat[i][k]);
max_i_row = i;
}
}
// If the largest entry is 0, the system of equations either has no solutions or infinitely many solutions.
if (max_i == 0) {
return 1;
}
// If a larger potential k value exists, swap the two rows.
if (max_i_row != k) {
swap_rows(mat, k, max_i_row);
}
// Add multiples of the kth row to each of the below columns in order to make all of the entries beneath k 0.
for (int i = k+1; i < N; i++) {
double m = -mat[i][k] / mat[k][k];
for (int j = 0; j <= N; j++) {
mat[i][j] += m * mat[k][j];
}
}
}
return 0;
}
We can now update our main function to use the new function, checking for whether the system could actually be solved or not.
int main() {
double points[] = {0, 2, 1, 8, 4, 4, 5, 4, 7, 6};
int num_points = 5;
double** mat = generate_matrix(points, num_points);
int err = gaussian_elimination(mat, num_points);
if (err == 1) {
printf("Could not solve.\n");
}
print_matrix(mat, num_points);
free_matrix(mat, num_points);
return 0;
}
Now, again assuming that you're using the same numbers as me, your matrix should look like this.
$$ \left[ \begin{array}{lr} 6.000 & 2.000 & 0.000 & 0.000 & -6.000 & -2.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 2.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 1.000 & 0.000 & 0.000 & -1.000 & -1.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 1.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 64.000 & 16.000 & 4.000 & 1.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & -4.000 & -2.000 & -0.750 & -48.000 & -8.000 & -1.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.562 & 0.844 & -9.000 & -1.500 & -0.188 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & -0.812 & -6.667 & -1.111 & -0.139 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 125.000 & 25.000 & 5.000 & 1.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & -5.000 & -2.000 & -0.600 & -75.000 & -10.000 & -1.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & -0.505 & -0.380 & -12.462 & -1.662 & -0.166 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & -0.061 & 20.122 & 4.683 & 0.668 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 343.000 & 49.000 & 7.000 & 1.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 7.143 & 2.449 & 0.636 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.514 & 0.233 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & -0.000 & 0.000 & 0.000 & 0.032 \end{array} \right] \left[ \begin{array}{lr} 0.000 \\ 0.000 \\ 0.000 \\ 2.000 \\ 4.000 \\ -3.000 \\ 7.375 \\ -0.065 \\ 4.000 \\ -2.400 \\ -6.547 \\ -4.230 \\ 6.000 \\ 1.813 \\ 0.281 \\ 0.322 \end{array} \right] $$
From here, you could solve for the coefficients by hand, or at least the last 4, and check that it works properly.
$$d_4 = 0.322 / 0.032 = 10.063$$
$$c_4 = (0.281 - 0.233*10.063) / 0.514 = -4.015$$
$$b_4 = (1.813 - 0.636*10.063 - 2.449*-4.015) / 7.143 = 0.734$$
$$a_4 = (6 - 1*10.063 - 7*-4.015 - 49*0.734) / 343 = -0.035$$
With these, you can plug \(a_4x^3 + b_4x^2 + c_4x + d_4\) into a graphing calculator such as Desmos alongside the points. The resulting graph does in fact connect the last two points as it is supposed to. The fit isn't perfect, but only because we've been rounding our results.
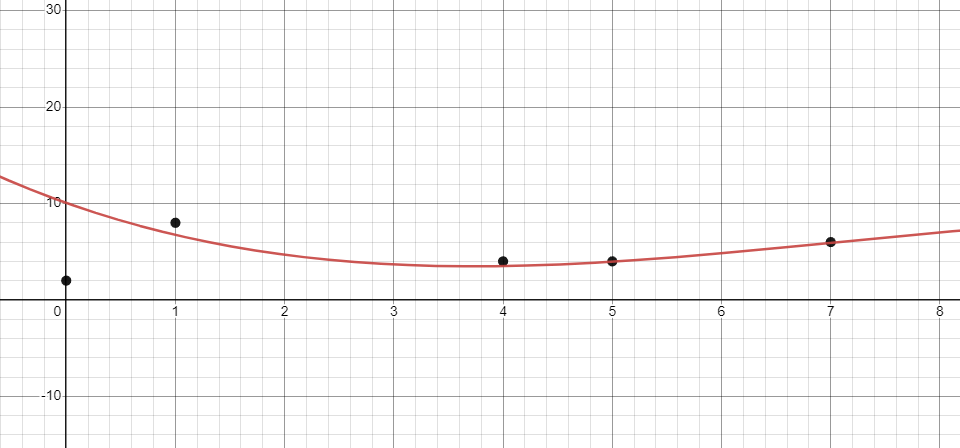
Of course, if your computer had to wait for you to perform the backwards substitution, it wouldn't be very performant. Not to mention scalability. So let's write that function next. We'll calculate the values of all of the unknowns and leave them in the extra column of the matrix that represents the right-hand side. We iterate over the right-hand side from the bottom up. For each one, we iterate over all of the values to the left of it except the leading entry, and multiply each by the corresponding unknown which we would have already calculated. The sum of these products is subtracted from the value in the right-hand side. After that, we divide the value in the right-hand side by the leading entry in its row. The value is now equal to the corresponding unknown.
After the algorithm has run, all of the unknowns will be in the right-most column with \(a_1\) at the top and \(d_{n-1}\) at the bottom.
// Solve for the unknowns in reverse order. The results are placed in column N in the RHS.
void back_substitution(double** mat, int num_points) {
int N = num_points * 4 - 4;
// Solve from bottom to top
for (int i = N-1; i >= 0; i--) {
// Subtract all previous terms.
for (int j = N-1; j > i; j--) {
mat[i][N] -= mat[j][N] * mat[i][j];
}
mat[i][N] /= mat[i][i];
}
}
Now, we can rewrite our main function once more to look like this:
int main() {
double points[] = {0, 2, 1, 8, 4, 4, 5, 4, 7, 6};
int num_points = 5;
double** mat = generate_matrix(points, num_points);
int err = gaussian_elimination(mat, num_points);
if (err == 1) {
printf("Could not solve.\n");
print_matrix(mat, num_points);
}
else {
back_substitution(mat, num_points);
print_matrix(mat, num_points);
}
free_matrix(mat, num_points);
return 0;
}
After this, our matrix should look like the following:
$$ \left[ \begin{array}{lr} 6.000 & 2.000 & 0.000 & 0.000 & -6.000 & -2.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 2.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 1.000 & 0.000 & 0.000 & -1.000 & -1.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 1.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 64.000 & 16.000 & 4.000 & 1.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & -4.000 & -2.000 & -0.750 & -48.000 & -8.000 & -1.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.562 & 0.844 & -9.000 & -1.500 & -0.188 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & -0.812 & -6.667 & -1.111 & -0.139 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 125.000 & 25.000 & 5.000 & 1.000 & 0.000 & 0.000 & 0.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & -5.000 & -2.000 & -0.600 & -75.000 & -10.000 & -1.000 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & -0.505 & -0.380 & -12.462 & -1.662 & -0.166 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & -0.061 & 20.122 & 4.683 & 0.668 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 343.000 & 49.000 & 7.000 & 1.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 7.143 & 2.449 & 0.636 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.514 & 0.233 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & 0.000 & -0.000 & 0.000 & 0.000 & 0.032 \end{array} \right] \left[ \begin{array}{lr} -1.136 \\ 0.000 \\ 7.136 \\ 2.000 \\ 0.573 \\ -5.126 \\ 12.262 \\ 0.291 \\ -0.514 \\ 7.925 \\ -39.945 \\ 69.901 \\ -0.035 \\ 0.728 \\ -3.959 \\ 9.924 \end{array} \right] $$
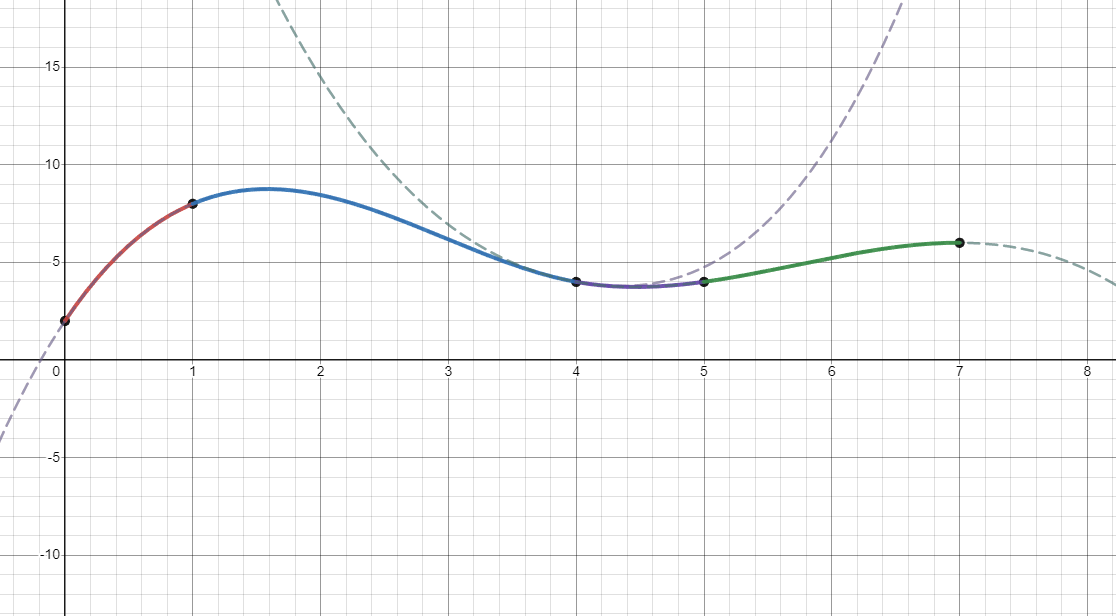
Plugging in the values into the equations produces the following graphs. The dashed lines are the individual cubic equations in their entirety, wheres the solid lines are the segments of those cubics which are actually used in the spline.
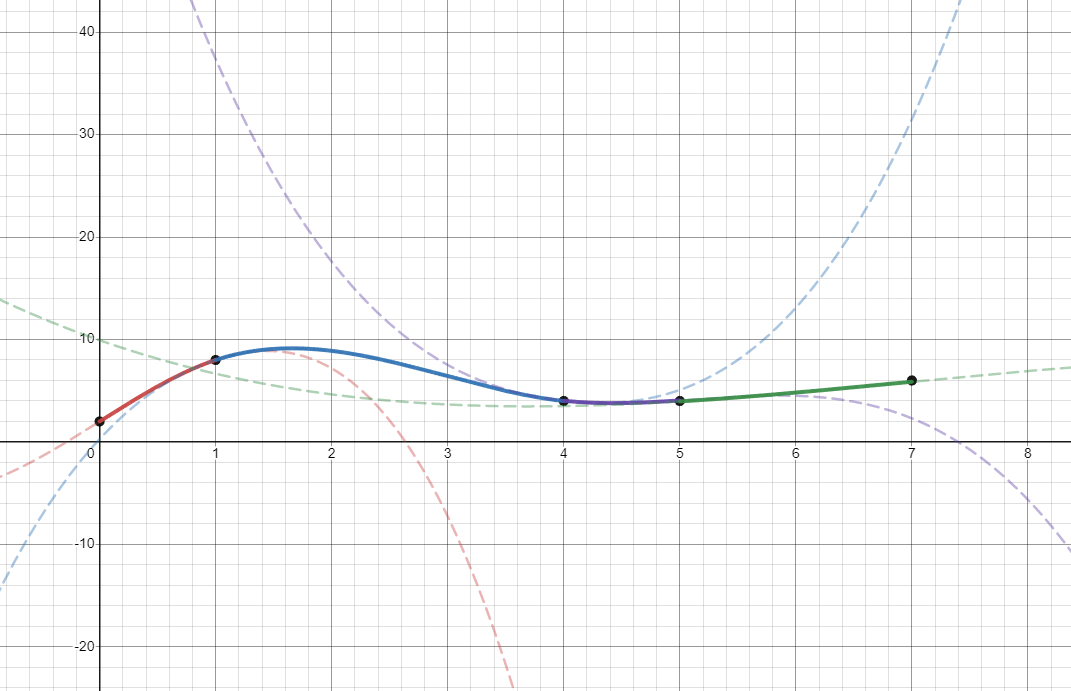
Boundary Conditions
If you recall, we produced our existing splines with the "natural" boundary conditions. However, we could choose any sort of boundary condition. The natural boundary conditions are given below.
$$C_1''(x_1) = 0$$
$$C_{n-1}''(x_n) = 0$$
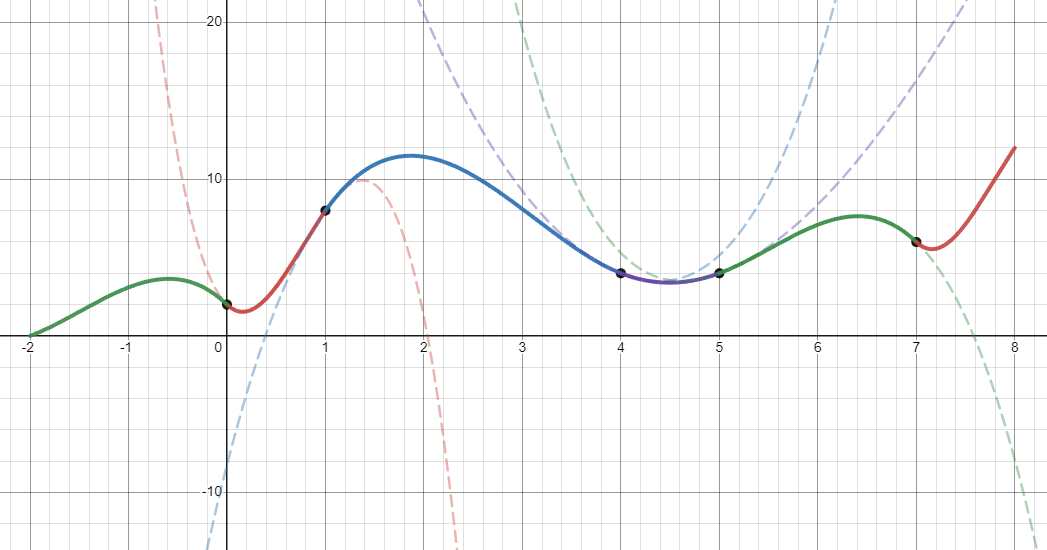
Alternatively, we could require that the first and second derivative is the same as the first and last point. This would allow us to repeat the spline without a break in the curve. The periodic equations are given below.
$$C_1'(x_1) = C'_{n-1}(x_n)$$
$$C_1''(x_1) = C''_{n-1}(x_n)$$
Using the same points as before, the periodic boundary condition produced the following graph. I've included an extra copy of the first and last segment on either side.
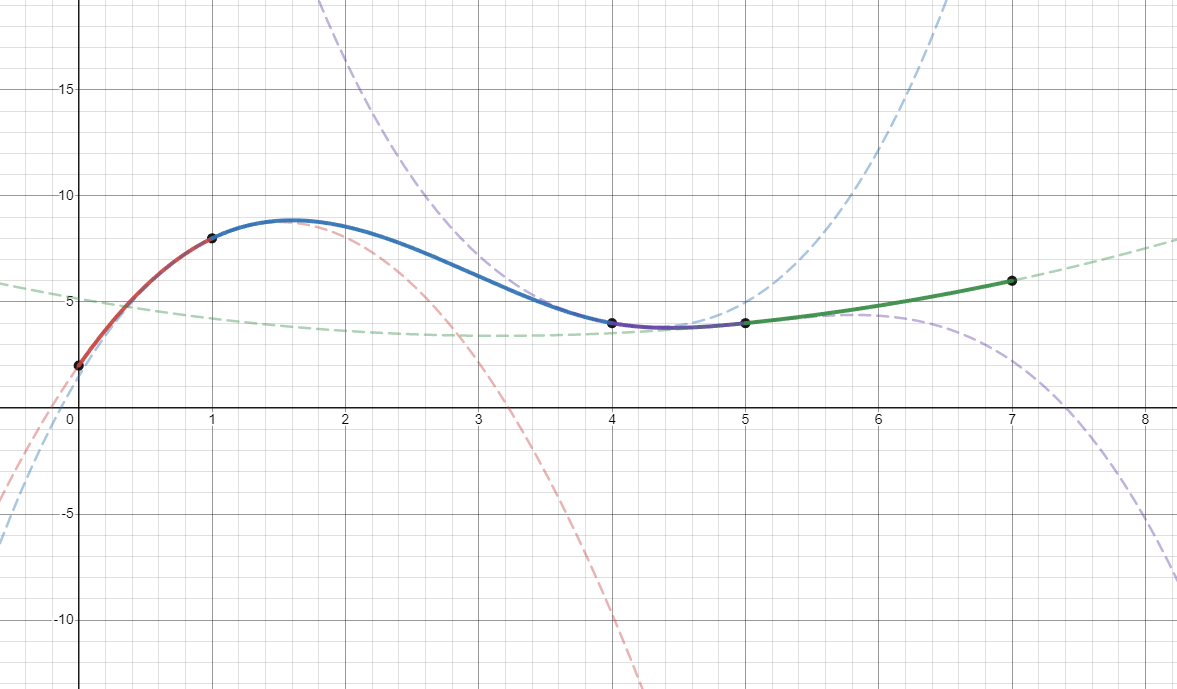
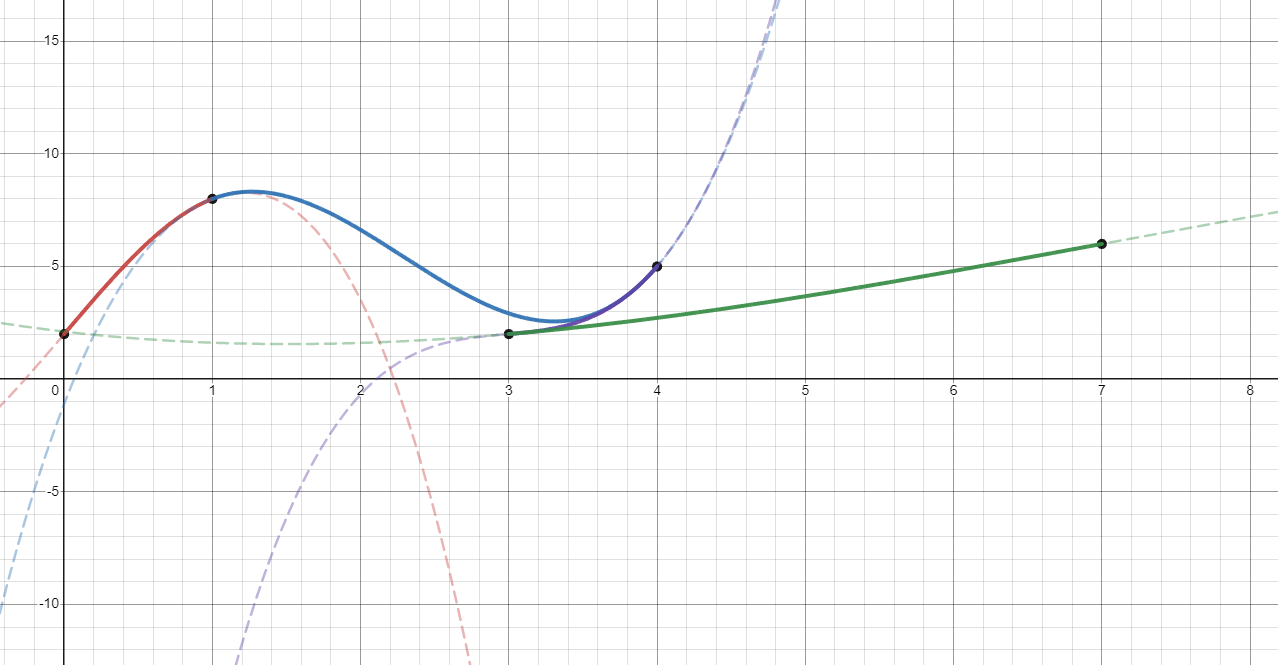
Another boundary condition we could use is the quadratic boundary condition. by setting \(a_1\) and \(a_n\) to zero, the first and last segments will be quadratics instead of cubics. You can see that the dashed green and red lines in the curves below are in fact quadratics.
$$a_1 = 0$$
$$a_n = 0$$
Finally, I'll discuss the Not-A-Knot boundary condition, which requires the third derivative of the first two segments to be the same at the point where they meet. The same requirement is made of the last two segments. Notably, this ensures that the first and second segment are actually a part of the same cubic function. The same is true of the last two segments as well.
$$a_1 = a_2$$
$$a_n = a_{n-1}$$
Breaking the Rules
You don't actually have to specify the points from left to right. If you don't, the resulting spline won't be a function (much less differentiable), but the algorithm will still find a valid solution.
Useful Resources
Below is a list of resources that I found particularly helpful in my research.